|
|
www.juezyverdugo.es
--- contacto@juezyverdugo.es
|
|
3
- Febrero - 2021
|
>>>> Juez y verdugo > Tienda
|
|
|
--------------------------------------------------------------------------------------------------------------
Las ecuaciones se usan desde tiempos muy remotos. Ya en el XVII a.C. los matemáticos de Mesopotamia y de Babilonia sabían resolver ecuaciones. En el siglo XVI a.C. los matemáticos egipcios desarrollaron un álgebra muy elemental que usaron para resolver problemas de su día a día que tenían que ver con la repartición de víveres, de cosechas y de materiales. El método de resolución que usaban se llamaba el "método de la falsa posición", en el que se pone de manifiesto que, aunque no tenían notación algebraica todavía, sí usaban la palabra "aha" (que significa montón o pila) para representar la incógnita. El apogeo de la cultura egipcia se produjo hacia el año 2500 a.C., época en la que los faraones hicieron construir las grandes pirámides y continuó hasta que Alejandro Magno los conquistó en el año 331 a.C. El escrito más conocido realizado por los antiguos egipcios se llama "Papiro de Rhind o de Ahmes" que contiene, sobre todo, problemas cotidianos de tipo aritmético. Aunque fue escrito por Ahmes (sobre el 1770 a.C.), también se le conoce como Papiro de Rhind debido a un anticuario escocés, Hery Rhind, quien lo compró en el año 1858 d.C. en una ciudad comercial a orillas del Nilo. Sobre el siglo I d.C. los matemáticos griegos escribieron también sobre métodos de resolución de ecuaciones. Y los matemáticos griegos, a excepción de Diofanto (250 d.C.), se dedicaron mucho más a la geometría que al álgebra. Hasta el siglo III d.C. el matemático griego Diofanto de Alejandría no publica su libro "Aritmética" en el que, por primera vez en la historia de las matemáticas griegas, se trataron de forma rigurosa las ecuaciones de primer grado.
Diofanto de Alejandría vivió en el siglo III o en el IV, fue un antiguo matemático griego. Es considerado "el padre del álgebra". Fue el autor de una serie de libros llamados Arithmetica, muchos de los cuales ahora se han perdido. Diofanto introduce un simbolismo algebraico muy simple basado en representar la incógnita con la primera sílaba de la palabra griega arithmos (que significa número). Aunque era una notación simbólica muy rudimentaria, se puede considerar a Diofanto como uno de los precursores del álgebra moderna, a pesar de que su libro se titule Aritmética y no Álgebra. Otro avance importante sobre ecuaciones lo desarrolló el matemático y astrónomo árabe Al-khwarizmi (siglo IX d.C.). Su principal aportación fue la de introducir en Europa el sistema de numeración decimal o indoarábigo e investigar sobre los principios fundamentales del álgebra.
Al-khwarizmi nació en Bagdad en la edad de oro de la cultura islámica. Su obra fue traducida al latín en el siglo XII d.C. dando origen al término "álgebra". Abu Abdallah Muhammad Ibn Musa Al-Jwarizmi, conocido generalmente como al-Juarismi, y latinizado antiguamente como Algorithmi, fue un matemático, astrónomo y geógrafo persa. Fue astrónomo y jefe de la Biblioteca de la Casa de la Sabiduría de Bagdad, alrededor de 820. En ella se pueden contemplar una serie de reglas aritméticas para resolver ecuaciones de primer y segundo grado. Y se puede decir que el método de resolución de tales ecuaciones no se diferencia demasiado al usado por nosotros en la actualidad. Sin embargo, hubo que esperar hasta la denominada Edad Moderna para que los matemáticos franceses Vieta (siglo XVI d.C.) y Descartes (siglo XVII) dotaran al álgebra del lenguaje simbólico casi idéntico al que usamos hoy en día. Una curiosidad interesante de resaltar es la llegada del símbolo de la igualdad (=), introducido por el matemático inglés Robert Recorde en el año 1557 d.C. Robert lo usó argumentando que no hay nada más igual que dos rectas paralelas.
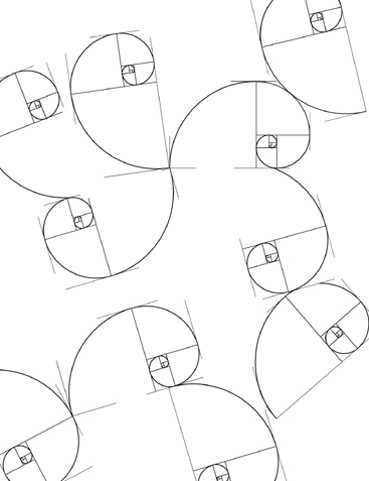
En matemáticas, la sucesión o serie de Fibonacci es la siguiente sucesión infinita de números naturales: 1 , 1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , 55 , 89 , 144 , 233 , 377 , 610 , 987 , 1597 … La sucesión comienza con los números 0 y 1 y a partir de estos, «cada término es la suma de los dos anteriores», es la relación de recurrencia que la define. A los elementos de esta sucesión se les llama hijos de Fibonacci. Esta sucesión fue descrita en Europa por Leonardo de Pisa, matemático italiano del siglo XIII también conocido como Fibonacci. Tiene numerosas aplicaciones en ciencias de la computación, matemática y teoría de juegos. También aparece en configuraciones biológicas, como por ejemplo en las ramas de los árboles, en la disposición de las hojas en el tallo, en las flores de alcachofas y girasoles, en las inflorescencias del brécol romanesco, en la configuración de las piñas de las coníferas, en la reproducción de los conejos y en cómo el ADN codifica el crecimiento de formas orgánicas complejas. De igual manera, se encuentra en la estructura espiral del caparazón de algunos moluscos, como el nautilus.
Según muchos investigadores, el frontis de la Catedral de Notre Dame -que resistió las llamas del incendio reciente- esconde uno de los más grandes secretos de la arquitectura antigua: el de las proporciones áureas. Sin embargo, las voces escépticas al respecto no son pocas. El Taj Mahal o el Partenon son otros ejemplos.
--------------------------------------------------------------------------------------------------------------
--------------------------------------------------------------------------------------------------------------
--------------------------------------------------------------------------------------------------------------
--------------------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------------------- |
|